8 - Triangle et cercle - Cours
Définitions :
Un triangle est un polygone à 3 côtés.Un triangle isocèle est un triangle possédant deux côtés égaux.Un triangle équilatéral est un triangle possédant trois côtés égaux.Un triangle rectangle est un triangle possédant un angle droit.
Remarque :
Un triangle peut être isocèle et rectangle.
Exemple :
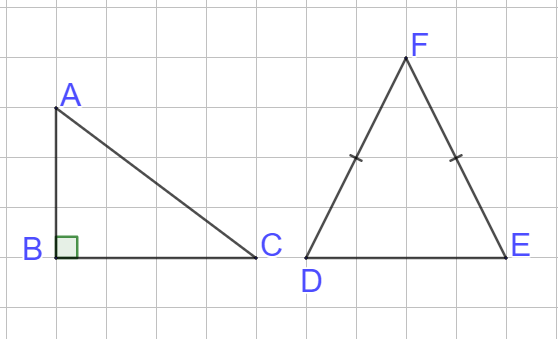Le triangle ABC est rectangle en B et le triangle DEF est isocèle en F. La base du triangle DEF est le côté [DE]
Le triangle ABC est rectangle en B et le triangle DEF est isocèle en F. La base du triangle DEF est le côté [DE]
Propriété :
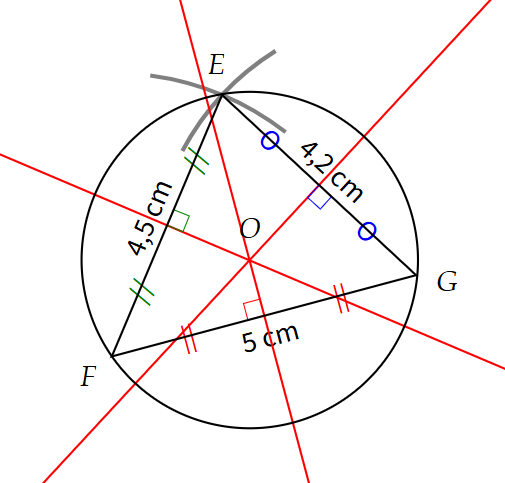
Les médiatrices des côtés d'un triangle se coupent en un même point qui est le centre du cercle circonscrit du triangle.
Propriété :
Un triangle isocèle possède deux angles égaux à sa base.Un triangle équilatérale possède trois angles égaux qui mesurent 60°.
Exemple :
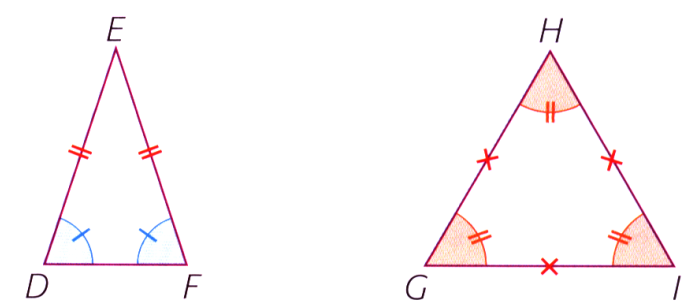Le triangle DEF est isocèle en E, donc \( \widehat{EDF} = \widehat{EFD} \).Le triangle GHI est équilatéral, donc \( \widehat{GHI} = \widehat{GIH} = \widehat{IGH} = 60° \)
Le triangle DEF est isocèle en E, donc \( \widehat{EDF} = \widehat{EFD} \).Le triangle GHI est équilatéral, donc \( \widehat{GHI} = \widehat{GIH} = \widehat{IGH} = 60° \)
Propriété :
Un triangle est constructible si la somme des longueurs des deux plus petits côtés est plus grande que la longueur du plus grand côté.
Exemple
Dans le triangle BOL avec BO = 5 cm, BL = 7 cm et LB = 10 cm , [LB] est le plus grand côté. BO+BL=5+7=12 et 12>10 donc le triangle BOL est constructible.Dans le triangle RAT avec RA = 10 cm AT = 5 cm et RT = 3 cm , [RA] est le plus grand côté. AT+RT=5+3=8 et 8<10 donc le triangle RAT n'est pas constructible.
Définition :
Le rayon d'un cercle est le segment reliant son centre à son bord. Le diamètre d'un cercle est le segment d'extrémités deux points du cercle passant par le centre.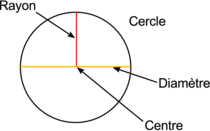 
Propriété :
Un diamètre est composé de deux rayons.