Chapitre 1 : Nombres relatifs

Définition :
Un nombre relatif est composé d'un signe - ou + et d'un nombre appelé distance à zéro.
Un nombre avec un signe + est appelé positif. Un nombre avec un signe - est appelé négatif.
Exemple :
+42 ; +3,08 ; +0,0003 sont des nombres positifs.
-23 ; -4,7 ; -0,001 sont des nombres négatifs.
Remarque :
Écrire 42 est équivalent à écrire +42.

0 est le seul nombre à la fois positif et négatif.
Définition :
On appelle droite graduée une droite sur laquelle on fixe un point appelé origine de la droite graduée, un sens, et une unité de longueur.

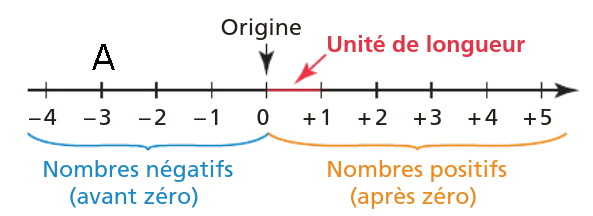
On dit que le point A a pour abscisse -3, et on note A(-3)
Définition :
L'opposé d'un nombre est ce même nombre avec le signe opposé.
Exemple :
L'opposé de -15,3 est +15,3 (autrement noté 15,3).
L'opposé de 9,8 est -9,8.
Propriété :
Lorsqu'on additionne deux nombres opposés, la somme vaut 0.
Exemple :
La somme de 3 et de -3 vaut 0, car -3 et 3 sont opposés.
La somme de -48,9 et de 48,9 vaut 0, car -48,9 et 48,9 sont opposés.
Propriété :
Pour comparer deux nombres relatifs, il existe 3 cas :
  • Entre deux nombres négatifs, celui qui est le plus grand a la plus petite distance à zéro.
  • Entre deux nombres positifs, celui qui est le plus grand a la plus grande distance à zéro.
  • Entre un nombre positif et un négatif, celui qui est le plus grand est le nombre positif.
Exemple :
+2 < +12 car ce sont deux nombres positifs et +12 a la plus grande distance à zéro.
-10 < +14 car +14 est positif et -10 négatif.
-19 < -12 car ce sont deux nombres négatifs et -19 a la plus grande distance à zéro.
Définition :
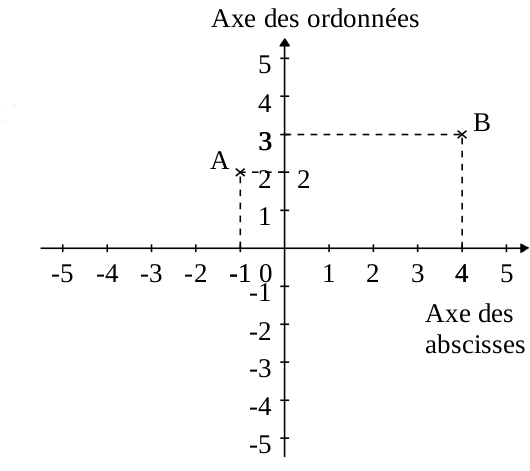
Un repère orthogonal du plan est composé de deux axes perpendiculaires en un point appelé origine : à l'horizontale l'axe des abscisses et à la verticale l'axe des ordonnées.
Définition :
Chaque point est repéré par deux nombres appelés coordonnées du point. Le premier est appelé son abscisse, et le second son ordonnée.
Exemple :
Ici, A a pour abscisse -1 et ordonnée 2.
On dit que les coordonnées de A sont (-1; 2). On note cela : A(-1; 2)
B a pour abscisse 4 et ordonnée 3.
On dit que les coordonnées de B sont (4; 3).
On note cela : B(4; 3)