Chapitre 5 : Division euclidienne

Définition :
Une division euclidienne est un nombre appelé dividende divisé par un nombre appelé diviseur.
Le résultat d'une division euclidienne est à la fois le quotient et le reste.
Exemple :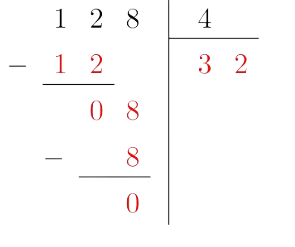
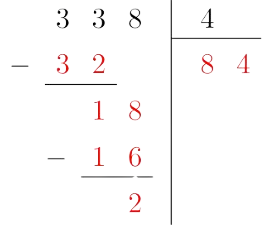
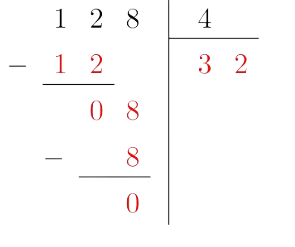
Remarque :
Comme le reste de la division euclidienne de 128 par 4 est 0, on peut dire que :
  • 128 est un multiple de 4 : autrement dit « 128 est dans la table de 4 » ;
  • 128 est divisible par 4 : on peut diviser 128 par 4 sans qu'il y aie de reste ;
  • 4 est un diviseur de 128.
Propriété :
Il existe différents critères de divisibilités. Un nombre est divisible par :
  • 2 si son chiffre des unités est 0; 2; 4; 6 ou 8
  • 3 si la somme de ses chiffres est un multiple de 3
  • 4 si ses deux derniers chiffres forment un multiple de 4
  • 5 si son chiffre des unités est 0 ou 5
  • 9 si la somme de ses chiffres est un multiple de 9
  • 10 si son chiffre des unités est 0.
Exemple :
375 n'est pas un multiple de 2 car le chiffre des unités est 5. Pour la même raison, c'est un multiple de 5 mais pas un multiple de 10.
3+7+5=15 et 15 est un multiple de 3 mais pas un multiple de 9, donc 375 est un multiple de 3 mais pas un multiple de 9.
75 n'est pas un multiple de 4, donc 375 n'est pas un multiple de 4.