Chapitre 2 : Rappels de géométrie
Propriété :
La droite passant par les points A et B est notée (AB).
Le segment d'extrémités les points A et B se note [AB].
La longueur du segment [AB] se note AB.
La demie-droite d'origine A passant par B se note [AB).
Le segment d'extrémités les points A et B se note [AB].
La longueur du segment [AB] se note AB.
La demie-droite d'origine A passant par B se note [AB).
Exemple :
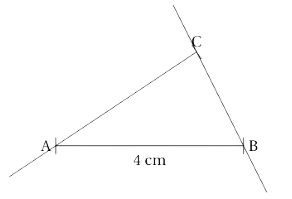 On peut voir ici le segment [AB], la droite (BC) et la demie-droite [CA).
On peut voir ici le segment [AB], la droite (BC) et la demie-droite [CA).
De plus, AB = 4cm
 On peut voir ici le segment [AB], la droite (BC) et la demie-droite [CA).
On peut voir ici le segment [AB], la droite (BC) et la demie-droite [CA). De plus, AB = 4cm
Propriété :
Des points sont dits alignés si on peut tracer une droite passant par ces points.
Définition :
Dire qu'un point appartient à une droite, un segment ou une demie droite signifie qu'il est dessus. On note ∈ pour "appartient" et ∉ pour "n'appartient pas".
Définition :
Deux droites sont dites sécantes si elles se coupent en un point appelé point d'intersection.
Deux droites non sécantes sont dites parallèles.
Deux droites formant un angle droit sont dites perpendiculaires.
Deux droites non sécantes sont dites parallèles.
Deux droites formant un angle droit sont dites perpendiculaires.
Exemple :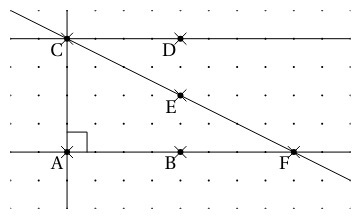 Les droites (CE) et (AB) sont sécantes en F.
Les droites (CE) et (AB) sont sécantes en F.
Les droites (AB) et (AC) sont perpendiculaires en A. On peut noter (AB) ⊥ (AC).
Les droites (AB) et (CD) sont parallèles. On peut noter (AB) ∥ (CD).
 Les droites (CE) et (AB) sont sécantes en F.
Les droites (CE) et (AB) sont sécantes en F.Les droites (AB) et (AC) sont perpendiculaires en A. On peut noter (AB) ⊥ (AC).
Les droites (AB) et (CD) sont parallèles. On peut noter (AB) ∥ (CD).
Méthode :
Tracer une droite perpendiculaire passant par un point :
Tracer une droite parallèle à une autre passant par un point :
Tracer une droite parallèle à une autre passant par un point :
Propriété :
Si une droite (d) est perpendiculaire à une droite (d1) et une droite (d2) parallèle à (d1), alors (d) et (d2) sont perpendiculaires.
Exemple :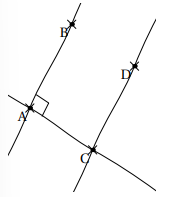 (AB) ⊥ (CA) et (AB) ∥ (CD) donc (CD) ⊥ (CA)
(AB) ⊥ (CA) et (AB) ∥ (CD) donc (CD) ⊥ (CA)
 (AB) ⊥ (CA) et (AB) ∥ (CD) donc (CD) ⊥ (CA)
(AB) ⊥ (CA) et (AB) ∥ (CD) donc (CD) ⊥ (CA)Propriété :
Si deux droites (d1) et (d2) sont parallèles à une même droite (d), alors (d1) et (d2) sont parallèles.
Exemple :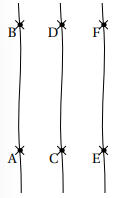 (AB) ∥ (CD) et (CD) ∥ (EF) donc (AB) ∥ (EF)
(AB) ∥ (CD) et (CD) ∥ (EF) donc (AB) ∥ (EF)
 (AB) ∥ (CD) et (CD) ∥ (EF) donc (AB) ∥ (EF)
(AB) ∥ (CD) et (CD) ∥ (EF) donc (AB) ∥ (EF)Propriété :
Si deux droites (d1) et (d2) sont perpendiculaires à une même droite (d), alors (d1) et (d2) sont parallèles.
Exemple :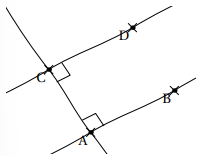 (AB) ⊥ (CA) et (CD) ⊥ (CA) donc (CD) ∥ (BA)
(AB) ⊥ (CA) et (CD) ⊥ (CA) donc (CD) ∥ (BA)
 (AB) ⊥ (CA) et (CD) ⊥ (CA) donc (CD) ∥ (BA)
(AB) ⊥ (CA) et (CD) ⊥ (CA) donc (CD) ∥ (BA)Remarque :
Propriétés version réduite :
1) Si (d) ⊥ (d₁) et (d₂) ∥ (d₁) alors (d) ⊥ (d₂)
2) Si (d) ∥ (d₁) et (d₂) ∥ (d₁) alors (d) ∥ (d₂)
3) Si (d) ⊥ (d₁) et (d₂) ⊥ (d) alors (d₁) ∥ (d₂)
1) Si (d) ⊥ (d₁) et (d₂) ∥ (d₁) alors (d) ⊥ (d₂)
2) Si (d) ∥ (d₁) et (d₂) ∥ (d₁) alors (d) ∥ (d₂)
3) Si (d) ⊥ (d₁) et (d₂) ⊥ (d) alors (d₁) ∥ (d₂)