Chapitre 8 : Tableau de proportionnalité
Définition :
Deux grandeurs sont dites proportionnelles lorsque l'on peut obtenir la deuxième à partir de la première en la multipliant par un même nombre, que l'on appelle coefficient de proportionnalité.
Exemple :
Le montant d'un plein d'essence est proportionnel au prix d'un litre d'essence : si un litre d'essence coûte 2€, 10 litres d'essence coûtent 20€.

Remarque :
Calculer le coefficient de proportionnalité revient à faire un retour à l'unité.
Exemple :
Si le prix de 10 kg de patates coûtent 15€, 1 kg de patates coûte


Propriété :
Dans un tableau de proportionnalité, l'égalité des produits en croix est vérifiée.
Exemple :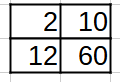 2 × 60 = 120 et 12 × 10 = 120 donc 2 × 60 = 12 × 10
2 × 60 = 120 et 12 × 10 = 120 donc 2 × 60 = 12 × 10
 2 × 60 = 120 et 12 × 10 = 120 donc 2 × 60 = 12 × 10
2 × 60 = 120 et 12 × 10 = 120 donc 2 × 60 = 12 × 10Propriété :
On peut utiliser l'égalité des produits en croix pour calculer une quatrième proportionnelle.
Exemple :

Propriété :
Pour vérifier si un tableau est un tableau de proportionnalité, on doit vérifier s'il existe un coefficient de proportionnalité.
Exemple :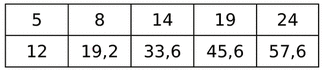
Les quotients sont tous égaux, donc le coefficient de proportionnalité est donc 2,4, donc c'est bien un tableau de proportionnalité.
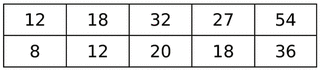
Les quotients ne sont pas tous égaux, donc le tableau n'est pas un tableau de proportionnalité.

Les quotients sont tous égaux, donc le coefficient de proportionnalité est donc 2,4, donc c'est bien un tableau de proportionnalité.

Les quotients ne sont pas tous égaux, donc le tableau n'est pas un tableau de proportionnalité.
Remarque :
On peut calculer des pourcentages grâce à la proportionnalité.
Exemple :
Dans une classe de 29 élèves, 3 ont fait une nuit blanche à Nouvel An.  soit
soit
 soit
soit