Chapitre 7 : Division décimales

Propriété :
La division décimale permet, à partir d'un dividende et d'un diviseur, d'obtenir soit un quotient décimal exact (nombre de chiffres après la virgule défini), soit une valeur approchée du quotient (nombre de chiffres après la virgule infini).
Exemple :
On obtient un reste de 0, donc le quotient est exact.
Méthode :
Donner une valeur approchée à l’unité, au dixième, au centième… d’un nombre décimal, c’est couper au rang indiqué puis :
  • si le chiffre qui suit est 5, 6, 7, 8 ou 9, on augmente de 1 le dernier chiffre du nombre coupé
  • si le chiffre qui suit est 0, 1, 2, 3 ou 4, on garde le nombre coupé
Exemple :
  • L’arrondi à l’unité de 17,527 est 18
  • L’arrondi à l’unité de 17,493 est 17
  • L’arrondi au dixième de 17,527 est 17,5
  • L’arrondi au dixième de 17,493 est 17,5
Propriété :
Lorsque, dans une division, le reste se répète, le quotient a un nombre infini de chiffres après la virgule. Nous devons donc donner une valeur approchée du quotient.
Exemple :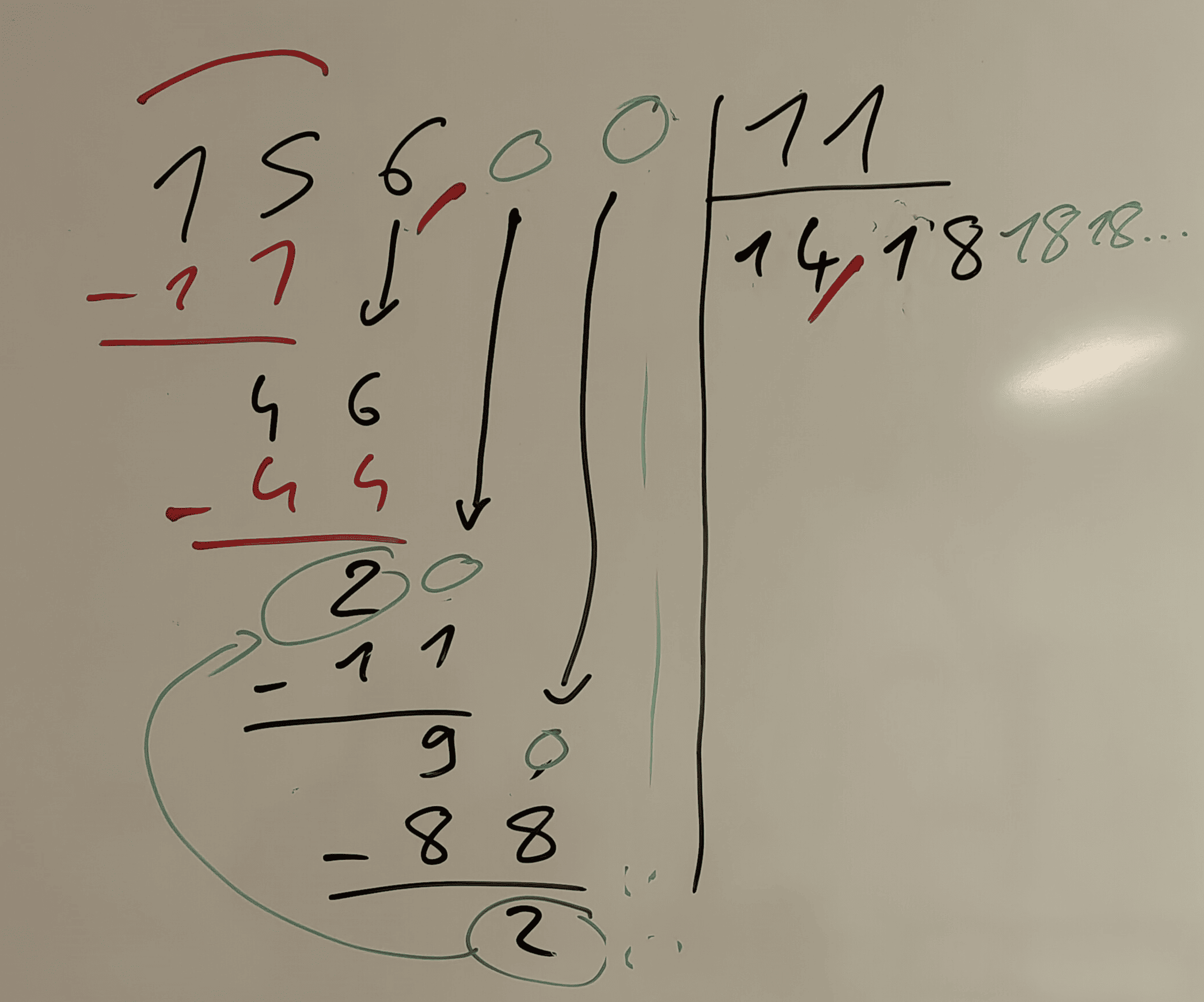
Le quotient de la division décimale de 156 par 11 au dixième près est 14,2 ; au centième près 14,18 et au millième près 14,182.