Chapitre 1 : Nombres décimaux
Propriété :
Un nombre décimal est composé d'une partie entière, à gauche de la virgule, et d'une partie décimale, à droite de la virgule.
Exemple :
24,56 a pour partie entière 24 et pour partie décimale 56.
8754,085 a pour partie entière 8754 et pour partie décimale 085.
8754,085 a pour partie entière 8754 et pour partie décimale 085.
Remarque :
Un nombre entier est un nombre décimale dont la partie décimale vaut 0. Par exemple, la partie entière de 23 est 23 et sa partie décimale 0, car on peut écrire 23,0.
Propriété :
Tout nombre décimal peut être inscrit dans un tableau de numération :
5 centaines et 3 unités = 503
78 dizaines =780
13 unités et 52 centièmes =13,52
6 unités de millions et 6 dix-millièmes = 6 000 000,000 6
5 centaines et 3 unités = 50378 dizaines =780
13 unités et 52 centièmes =13,52
6 unités de millions et 6 dix-millièmes = 6 000 000,000 6
Propriété :
Un nombre peut s'écrire de plusieurs façons.
Exemple :
Remarque :
On peut supprimer les zéros d'un nombre lorsqu'ils sont les derniers rangs de la partie décimale ou les premiers rangs de la partie entière : 00012,3 = 12,3 = 12,30000
Définitions :
Comparer deux nombres, c’est dire s’ils sont égaux ou si l’un est plus grand que l’autre.
Le signe < veut dire « plus petit que » et le signe > veut dire « plus grand que ».
Le signe < veut dire « plus petit que » et le signe > veut dire « plus grand que ».
Exemple :
17 < 20
10,065 > 10,056
10,065 > 10,056
Méthode :
Pour comparer deux nombres, on compare les chiffres au même rang en commençant par le chiffre le plus à gauche.
Si tous les chiffres sont égaux, les nombres sont égaux.
A partir du premier chiffre différent, le nombre ayant le chiffre le plus grand est le nombre le plus grand.
Si tous les chiffres sont égaux, les nombres sont égaux.
A partir du premier chiffre différent, le nombre ayant le chiffre le plus grand est le nombre le plus grand.
Définitions :
Ordre croissant veut dire « du plus petit au plus grand ».
Ordre décroissant veut dire « du plus grand au plus petit ».
Ordre décroissant veut dire « du plus grand au plus petit ».
Exemple :
Trions 10 ; 8 ; 15 ; 12 et 12,5
Dans l'ordre croissant : 8 < 10 < 12 < 12,5 < 15
Dans l'ordre décroissant : 15 > 12,5 > 12 > 10 > 8
Dans l'ordre croissant : 8 < 10 < 12 < 12,5 < 15
Dans l'ordre décroissant : 15 > 12,5 > 12 > 10 > 8
Definition :
Une demie-droite graduée est une demie droite sur laquelle on reporte une longueur régulièrement.
Chaque point de la droite peut être repéré par un nombre appelé abscisse.
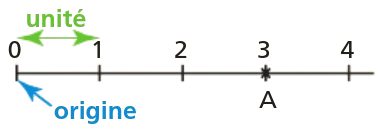On peut dire ici que le point A a pour abscisse 3, et on note A(3).
Chaque point de la droite peut être repéré par un nombre appelé abscisse.
On peut dire ici que le point A a pour abscisse 3, et on note A(3).Définition :
Encadrer un nombre, c’est écrire qu’il est compris entre deux nombres, l’un plus petit et l’autre plus grand.
Exemple :
Un encadrement de 12,3916 à l'unité près est : 12 < 12,3916 < 13
Un encadrement de 12,3916 au dixième près est : 12,3 < 12,3916 < 12, 4
Un encadrement de 12,3916 au centième près est : 12,39 < 12,3916 < 12,40
Un encadrement de 12,3916 au millième près est : 12,391 < 12,3916 < 12,392
Un encadrement de 12,3916 au dixième près est : 12,3 < 12,3916 < 12, 4
Un encadrement de 12,3916 au centième près est : 12,39 < 12,3916 < 12,40
Un encadrement de 12,3916 au millième près est : 12,391 < 12,3916 < 12,392