Chapitre 7 : Probabilités
Exercice 1 :
Liste les différentes issues possibles de ces expériences:
- Lancer une pièce de monnaie
- Choisir aléatoirement un jour dans la semaine
- Tirer une boule dans une urne contenant des boules bleues, des boules rouges et des boules vertes
- Lancer un dé à 10 faces numérotées de 1 à 10
Exercice 2 :
Une roue équilibrée de loterie est partagée en sept secteurs identiques sur lesquels les lettres du mot LOTERIE. On l’a fait tourner, elle s’immobilise et on observe la lettre obtenue.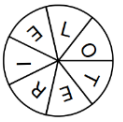
a) Liste les issues possibles.
b) Liste les issues des événements suivants et leurs probabilités :
A : "Obtenir la lettre E"
B : "Obtenir la lettre R"
C : "Obtenir une consonne"
D : "Obtenir une voyelle"
c) Lequel de ces événements est un événement certain ? Lequel est un événement impossible ?
E : "Obtenir un L, un T ou un Z"
F : "Obtenir un R et un T en même temps"
G : "Obtenir un L, un O, un T, un E, un R ou un I"
H : "Obtenir une des dix premières lettres de l'alphabet"
a) Liste les issues possibles.b) Liste les issues des événements suivants et leurs probabilités :
A : "Obtenir la lettre E"
B : "Obtenir la lettre R"
C : "Obtenir une consonne"
D : "Obtenir une voyelle"
c) Lequel de ces événements est un événement certain ? Lequel est un événement impossible ?
E : "Obtenir un L, un T ou un Z"
F : "Obtenir un R et un T en même temps"
G : "Obtenir un L, un O, un T, un E, un R ou un I"
H : "Obtenir une des dix premières lettres de l'alphabet"
Exercice 3 :
Dans le cadre de l'expérience "Lancer un dé à 10 faces numérotées de 1 à 10", liste les issues vérifiant l'évènement
A : "Obtenir un nombre paire",
B : 'Obtenir un nombre impaire",
C : "Obtenir un nombre à un chiffre",
D : "Obtenir un nombre à deux chiffres",
E : 'Obtenir un multiple de 1',
F : "Obtenir un multiple de 3",
G : "Obtenir un multiple de 4",
H : "Obtenir un multiple de 5",
I : 'Obtenir un nombre négatif",
J : "Obtenir un nombre positif".
A : "Obtenir un nombre paire",
B : 'Obtenir un nombre impaire",
C : "Obtenir un nombre à un chiffre",
D : "Obtenir un nombre à deux chiffres",
E : 'Obtenir un multiple de 1',
F : "Obtenir un multiple de 3",
G : "Obtenir un multiple de 4",
H : "Obtenir un multiple de 5",
I : 'Obtenir un nombre négatif",
J : "Obtenir un nombre positif".
Exercice 4 :
Calcule les probabilités des événements de l'exercice 3.
Exercice 5 :
Donne les événements contraire de l'exercice 3 et leurs probabilités.
Exercice 6 :
On considère l’urne suivante. On tire une boule aléatoirement.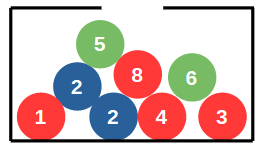 
a. Si on s’intéresse à la couleur de la boule, quelles sont les issues possibles ?
b. Si on s’intéresse au numéro écrit sur la boule, quelles sont les issues possibles ?
c. Cite un événement impossible.
d. Quelle est la probabilité de l’événement « Obtenir une boule rouge » ?
e. Écris l’événement contraire de l’événement « Obtenir une boule rouge ».
f. Déduis-en la probabilité de cet événement.
a. Si on s’intéresse à la couleur de la boule, quelles sont les issues possibles ? b. Si on s’intéresse au numéro écrit sur la boule, quelles sont les issues possibles ?
c. Cite un événement impossible.
d. Quelle est la probabilité de l’événement « Obtenir une boule rouge » ?
e. Écris l’événement contraire de l’événement « Obtenir une boule rouge ».
f. Déduis-en la probabilité de cet événement.
Exercice 7 :
Dans un jeu de 32 cartes, il y a quatre familles : les trèfles, les cœurs, les carreaux et les piques, et deux couleurs : rouge et noir. On décide de tirer au hasard une carte dans ce jeu.
a. Si l’on considère la couleur des cartes, cite les issues possibles.
b. Si l’on considère les familles, cite les issues possibles.
c. Cite un événement impossible.
d. Soit l'événement T : « La carte choisie est un trèfle. ». Calcule la probabilité de cet événement
e. Écris l’événement contraire T et calcule sa probabilité.
a. Si l’on considère la couleur des cartes, cite les issues possibles.
b. Si l’on considère les familles, cite les issues possibles.
c. Cite un événement impossible.
d. Soit l'événement T : « La carte choisie est un trèfle. ». Calcule la probabilité de cet événement
e. Écris l’événement contraire T et calcule sa probabilité.
Exercice 8 : (extrait du brevet)
Il y a dans une urne douze boules indiscernables au toucher, numérotées de 1 à 12. On veut tirer une boule au hasard.
a. Est-il plus probable d’obtenir un numéro pair ou bien un multiple de 3 ?
b. Quelle est la probabilité d’obtenir un numéro inférieur à 20 ?
c. On enlève de l’urne toutes les boules dont le numéro est un diviseur de 6. On veut à nouveau tirer une boule au hasard. Explique pourquoi la probabilité d’obtenir un numéro qui soit un nombre premier est alors 0,375.
a. Est-il plus probable d’obtenir un numéro pair ou bien un multiple de 3 ?
b. Quelle est la probabilité d’obtenir un numéro inférieur à 20 ?
c. On enlève de l’urne toutes les boules dont le numéro est un diviseur de 6. On veut à nouveau tirer une boule au hasard. Explique pourquoi la probabilité d’obtenir un numéro qui soit un nombre premier est alors 0,375.
Exercice 9 : (extrait du brevet)
Sam préfère les bonbons bleus. Dans son paquet de 500 bonbons, 150 sont bleus, les autres sont rouges, jaunes ou verts.
a. Quelle est la probabilité qu’il pioche au hasard un bonbon bleu dans son paquet ?
b. 20 % des bonbons de ce paquet sont rouges. Combien de bonbons rouges y a-t-il ?
c. Sachant qu’il y a 130 bonbons verts dans ce paquet, Sam a-t-il plus de chance de piocher au hasard un bonbon vert ou un bonbon jaune ?
a. Quelle est la probabilité qu’il pioche au hasard un bonbon bleu dans son paquet ?
b. 20 % des bonbons de ce paquet sont rouges. Combien de bonbons rouges y a-t-il ?
c. Sachant qu’il y a 130 bonbons verts dans ce paquet, Sam a-t-il plus de chance de piocher au hasard un bonbon vert ou un bonbon jaune ?