Chapitre 3 : Symétries
Définition :
Dire que deux points M et M' sont symétriques par rapport à une droite (d) signifie que la droite (d) coupe perpendiculairement le segment [MM'] en son milieu. On appelle la droite (d) l'axe de symétrie.
Exemple :
Méthode :
Tracer le symétrique d'un point : voir les vidéos sur monsieur-garcia.prof
Avec un quadrillage
Sans quadrillage avec une équerre :
Sans quadrillage avec une équerre et un compas :
Sans quadrillage avec un compas :
Avec un quadrillage
Sans quadrillage avec une équerre :
Sans quadrillage avec une équerre et un compas :
Sans quadrillage avec un compas :
Définition :
La symétrie centrale de centre O consiste à effectuer un demi-tour autour du point O. Le point O est appelé le centre de la symétrie, il est situé au milieu de tout segment reliant un point et son symétrique.
Exemple :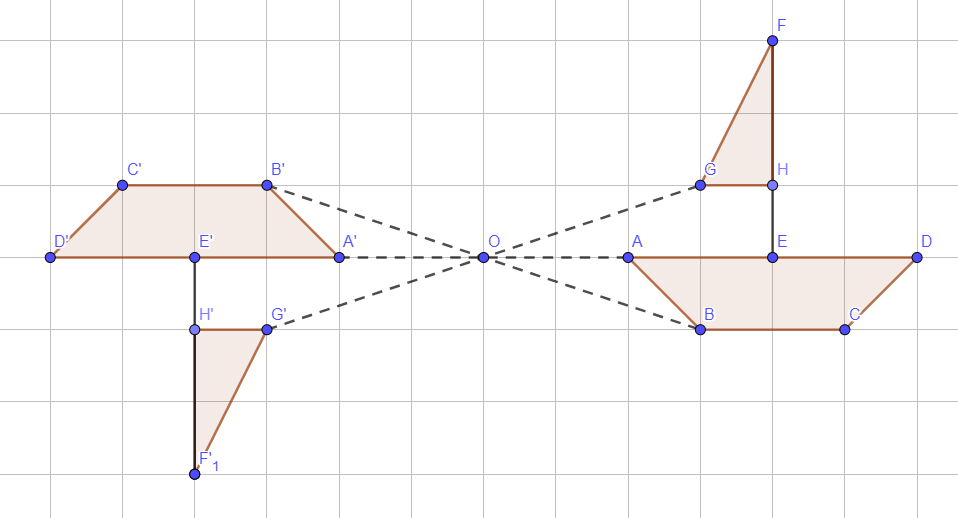

Méthode :
Propriété :
Les symétries conservent les angles, les longueurs et le parallélisme.
Exemple :
Dans l'exemple précédent, A', B', C', E' et H' sont respectivement les symétriques de A, B, C, E et H donc AE = A'E' , et (AE)⊥(HE) donc (A'E')⊥(H'E'); et (AE)∥(BC) donc (A'E')∥(B'C')