Chapitre 5 : Multiples et Diviseurs
Exercice 1 :
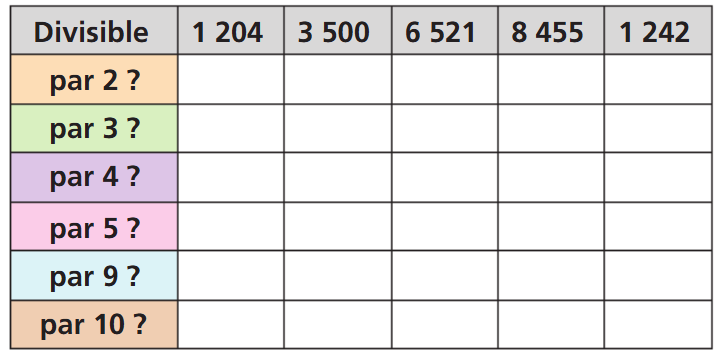
Exercice 2 :
Complète ce tableau par "oui" ou "non"

Exercice 3 :
1. Sram a 248 fragments stellaires. Pourra-t-il tous les mettre dans des groupes de 4 ?
2. Erret ramasse 525 météorites. Peut-il les répartir en paquets de 5 ?
3. Sunèv découvre 387 cristaux lunaires. Peut-elle les diviser en 3 parts égales ?
4. Enupten transporte 300 poussières d’étoiles. Peut-il les regrouper par 10 ?
5. Sunaru analyse 1 458 morceaux de comète. Peut-elle les regrouper par groupe de 9 ?
6. Retipuj collecte 732 petites planètes. Peut-il les compter 2 par 2 ?
7. Sram transporte 408 astéroïdes. Peut-il les ranger en groupes de 4 ?
8. Erret a trouvé 1 200 fragments de lune. Peut-elle les regrouper par dizaine ?
9. Sunèv ramasse 675 particules stellaires. Peut-elle les ranger en groupes de 5 ?
10. Enupten examine 927 morceaux de roche lunaire. Peut-il les examiner 3 par 3 ?
2. Erret ramasse 525 météorites. Peut-il les répartir en paquets de 5 ?
3. Sunèv découvre 387 cristaux lunaires. Peut-elle les diviser en 3 parts égales ?
4. Enupten transporte 300 poussières d’étoiles. Peut-il les regrouper par 10 ?
5. Sunaru analyse 1 458 morceaux de comète. Peut-elle les regrouper par groupe de 9 ?
6. Retipuj collecte 732 petites planètes. Peut-il les compter 2 par 2 ?
7. Sram transporte 408 astéroïdes. Peut-il les ranger en groupes de 4 ?
8. Erret a trouvé 1 200 fragments de lune. Peut-elle les regrouper par dizaine ?
9. Sunèv ramasse 675 particules stellaires. Peut-elle les ranger en groupes de 5 ?
10. Enupten examine 927 morceaux de roche lunaire. Peut-il les examiner 3 par 3 ?
Exercice 4 :
1. Écrire la liste de tous les diviseurs de 20.
2. Écrire la liste de tous les diviseurs de 10.
3. Écrire la liste de tous les diviseurs de 36.
4. Écrire la liste de tous les diviseurs de 22.
5. Écrire la liste de tous les diviseurs de 25.
6. Écrire la liste de tous les diviseurs de 15.
7. Écrire la liste de tous les diviseurs de 38.
8. Écrire la liste de tous les diviseurs de 45.
2. Écrire la liste de tous les diviseurs de 10.
3. Écrire la liste de tous les diviseurs de 36.
4. Écrire la liste de tous les diviseurs de 22.
5. Écrire la liste de tous les diviseurs de 25.
6. Écrire la liste de tous les diviseurs de 15.
7. Écrire la liste de tous les diviseurs de 38.
8. Écrire la liste de tous les diviseurs de 45.
Exercice 5 :
Sram doit répartir 36 croissants et 24 pains au chocolat dans des corbeilles.
Chaque corbeille doit avoir le même contenu.
1) Liste les diviseurs de 36 et de 24.
2) Souligne les diviseurs qu'ils ont en commun.
3) Quel est le nombre maximal de corbeilles que Sram peut faire, et quelles seront leurs compositions ?
Chaque corbeille doit avoir le même contenu.
1) Liste les diviseurs de 36 et de 24.
2) Souligne les diviseurs qu'ils ont en commun.
3) Quel est le nombre maximal de corbeilles que Sram peut faire, et quelles seront leurs compositions ?
Exercice 6 :
Sram a 90 étoiles et 54 comètes. Il veut faire des paquets contenant le même nombre d’étoiles et de comètes, sans qu’il reste d’étoiles ou de comètes.
a) Peut-il faire 3 paquets ? Et 10 ? Justifie. Si oui, donne la composition de chaque paquet.
b) Liste les diviseurs de 90 et 54.
c) Déduis-en le nombre maximum de paquets qu’il peut faire et leurs compositions.
a) Peut-il faire 3 paquets ? Et 10 ? Justifie. Si oui, donne la composition de chaque paquet.
b) Liste les diviseurs de 90 et 54.
c) Déduis-en le nombre maximum de paquets qu’il peut faire et leurs compositions.
Exercice 7 :
Sram a 54 éclats stellaires et 18 morceaux de comète. Il souhaite les répartir en caisses ayant toutes la même quantité d’éclats et de morceaux, sans reste.
a) Peut-il faire 8 caisses ? Et 3 ? Justifie. Si oui, donne la composition de chaque caisse.
b) Liste les diviseurs de 54 et 18.
c) Déduis-en le nombre maximum de caisses qu’il peut faire et leurs compositions.
a) Peut-il faire 8 caisses ? Et 3 ? Justifie. Si oui, donne la composition de chaque caisse.
b) Liste les diviseurs de 54 et 18.
c) Déduis-en le nombre maximum de caisses qu’il peut faire et leurs compositions.
Exercice 9 :
Exercice 10 :
L’application utilisée en classe est accessible à tous et permet de réaliser de très jolies figures : http://nathanfriend.io/inspirograph/
1. a) Si la roue fixe a 60 dents et la roue mobile en a 30, combien faut-il faire de tours pour compléter le dessin ? Combien de tour sur elle même a fait la roue mobile ?
b) Simplifie la fraction
Comment interpréter cette fraction dans ce contexte ?
2. a) Si la roue fixe a 50 dents et la roue mobile en a 45, combien faut-il faire de tours pour compléter le dessin ? Combien de tour sur elle même a fait la roue mobile ?
b) Simplifie la fraction
3. Sans utiliser le site, si la roue fixe a 36 dents et la roue mobile en a 24 , combien faut-il faire de tours pour compléter le dessin ? Combien de tour sur elle même a fait la roue mobile ?
1. a) Si la roue fixe a 60 dents et la roue mobile en a 30, combien faut-il faire de tours pour compléter le dessin ? Combien de tour sur elle même a fait la roue mobile ?
b) Simplifie la fraction
Comment interpréter cette fraction dans ce contexte ?
2. a) Si la roue fixe a 50 dents et la roue mobile en a 45, combien faut-il faire de tours pour compléter le dessin ? Combien de tour sur elle même a fait la roue mobile ?
b) Simplifie la fraction
3. Sans utiliser le site, si la roue fixe a 36 dents et la roue mobile en a 24 , combien faut-il faire de tours pour compléter le dessin ? Combien de tour sur elle même a fait la roue mobile ?