Chapitre 4 : Réciproque du théorème de Pythagore
Théorème :
Dans un triangle, si le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux plus petits côtés, alors ce triangle est rectangle et le plus grand côté est l'hypoténuse.
Exemple :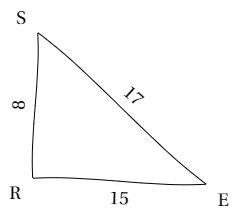
Dans le triangle ERS, [ES] est le plus grand côté.
D'une part, ES² = 17² = 289
D'autre part, ER²+RS²= 15² + 8² = 225 + 64 = 289
Donc ES²=ER²+RS², donc l'égalité de Pythagore est vérifiée, donc le triangle ERS est rectangle en R.
Dans le triangle ERS, [ES] est le plus grand côté. D'une part, ES² = 17² = 289
D'autre part, ER²+RS²= 15² + 8² = 225 + 64 = 289
Donc ES²=ER²+RS², donc l'égalité de Pythagore est vérifiée, donc le triangle ERS est rectangle en R.
Exemple :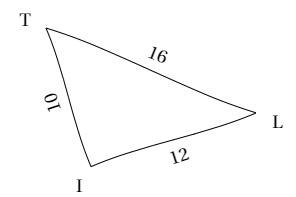
Dans le triangle LIT, [LT] est le plus grand côté.
D'une part, LT²=16²=256
D'autre part, LI²+IT²=12²+10²=144+100=244
Donc LT² ≠ LI²+IT², donc l'égalité de Pythagore n'est pas vérifiée, donc le triangle LIT n'est pas rectangle.
Dans le triangle LIT, [LT] est le plus grand côté.D'une part, LT²=16²=256
D'autre part, LI²+IT²=12²+10²=144+100=244
Donc LT² ≠ LI²+IT², donc l'égalité de Pythagore n'est pas vérifiée, donc le triangle LIT n'est pas rectangle.