Chapitre 8 : Fractions
Définition :
Une fraction est composée de deux nombres entiers. Le nombre du dessus est appelé numérateur, et celui du dessous dénominateur.
Exemple :
Dans la fraction
Propriété :
Pour lire une fraction, on lit d'abord le nombre du numérateur puis le nombre du dénominateur en ajoutant le suffixe "ièmes".
Exemple :
Remarque :
Il existe trois exceptions :
Propriété :
Les fractions permettent de décrire un partage ou une proportion.
Exemple :
Dans une classe de 20 élèves, il y a 12 filles et 8 garçons. On peut donc dire que les filles représentent
Méthode :
On peut lire l'abscisse d'un point sur la demi-droite graduée sous forme de fraction 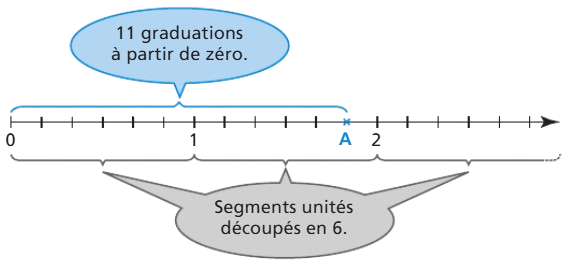 donc une graduation représente
donc une graduation représente
 donc une graduation représente
donc une graduation représente Propriété :
La valeur d'une fraction est le quotient de la division décimale du numérateur par le dénominateur.
Exemple :
Remarque :
Propriété :
Une fraction garde la même valeur si on multiplie ou divise son numérateur et son dénominateur par le même nombre.
Exemple :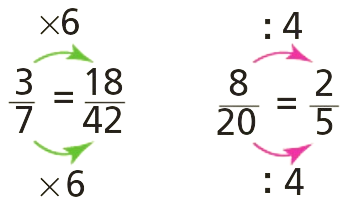
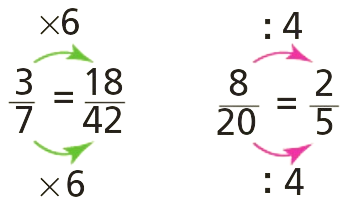
Remarque :
Diviser le numérateur et le dénominateur d'une fraction est appelé la simplifier, ou la réduire.
Définition :
Une fraction qu'on ne peut pas simplifier est dite irréductible.
Méthode :
Pour calculer la fraction d'une quantité, on multiplie par le numérateur et on divise par le dénominateur. Par exemple, pour calculer