Chapitre 6 : Angles et triangles

Propriété :
Un triangle est constructible si et seulement si la longueur du plus grand côté est inférieure à la somme des deux autres côtés.
Exemple :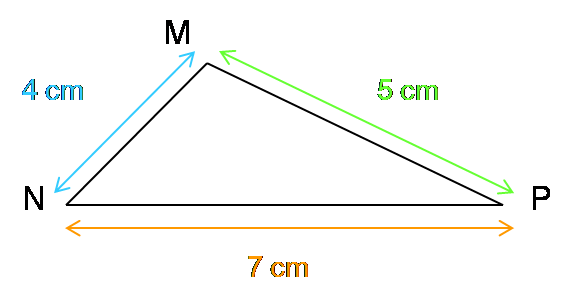
NP = 7 cm ; NM+MP=4+5=9; 9>7 donc le triangle est constructible.
Remarque :
Si la longueur du plus grand côté est égal à la somme des autres côtés, le triangle est dit plat.
Propriété :
La somme des angles d'un triangle est égale à 180°.
Exemple :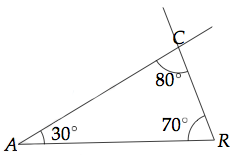
CAR^+ACR^+CRA^=30+80+70=180° donc le triangle est constructible
Propriété :
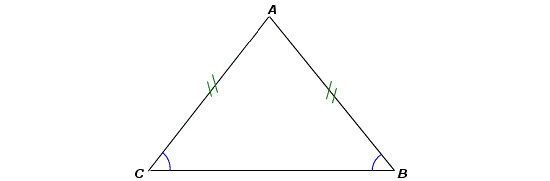
Un triangle isocèle possède deux angles égaux à sa base.
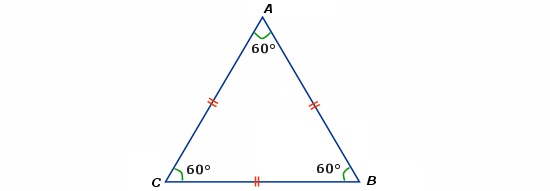
Un triangle équilatérale possède 3 angles égaux. Ils mesurent 60°.
Remarque :
Dans un triangle isocèle rectangle, un angle mesure 90° et les deux autres 45°.
Méthode :