Chapitre 9 : Triangle et cercle

Méthode :
Définition :
Un triangle est un polygone à trois côtés.
Définition :
Un triangle isocèle est un triangle possédant deux côtés égaux.
Un triangle équilatéral est un triangle possédant trois côtés égaux.
Exemple :
Le triangle ABC avec AB = AC = 4 cm et BC = 5cm est un triangle isocèle en A. On appelle [BC] la base du triangle ABC.
Le triangle DEF avec DE = Ef = FD = 3 cm est un triangle équilatéral.
Définition :
Un triangle rectangle est un triangle possédant un angle droit.
Exemple :
Le triangle GHI est rectangle en I.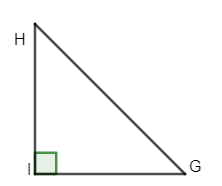
Remarque :
Un triangle peut être isocèle et rectangle, mais pas équilatéral et rectangle.
Propriété :
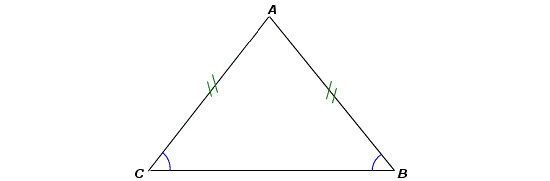
Un triangle isocèle possède deux angles égaux à sa base.
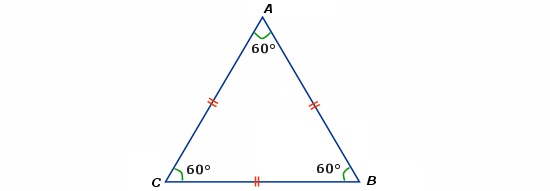
Un triangle équilatérale possède 3 angles égaux. Ils mesurent tous 60°.
Définition :
Le rayon d'un cercle est le segment reliant son centre à son bord. Le diamètre d'un cercle est le segment d'extrémités deux points du cercle passant par le centre.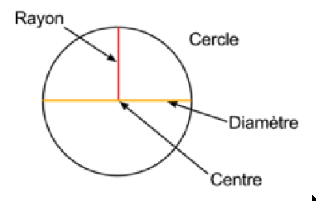
Propriété :
Un diamètre est composé de deux rayons.