Chapitre 10 : Angles et parallélismes

Définition :
Deux angles opposés par le sommet sont deux angles qui ont un sommet commun et qui ont leurs côtés dans le prolongement l'un de l'autre. Ces deux angles sont égaux.
Exemple :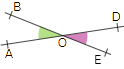
Les angles BOA^ et DOE^ sont opposés par rapport au point O.
Définition :
Lorsque deux droites sont coupées par une sécante, deux angles non adjacents, sont alternes internes si :
  • Ils sont situés de part et d’autre de la sécante
  • Ils sont situés à l’intérieur de la bande formée par les deux droites
Définition :
Lorsque deux droites sont coupées par une sécante, deux angles non adjacents, sont correspondant si :
  • Ils sont situés du même côté de la sécante
  • Ils sont situés à l’intérieur de la bande formée par les deux droites
Exemple :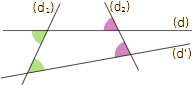
Les angles verts sont alternes-internes. Ils sont déterminés par les droites (d), (d') et la sécante (d1).
Les angles roses sont correspondants. Ils sont déterminés par les droites (d), (d') et la sécante (d2).
Propriété :
Si deux angles alternes-internes (ou correspondants) sont de même mesure, alors ils sont déterminés par des droites parallèles.
Exemple :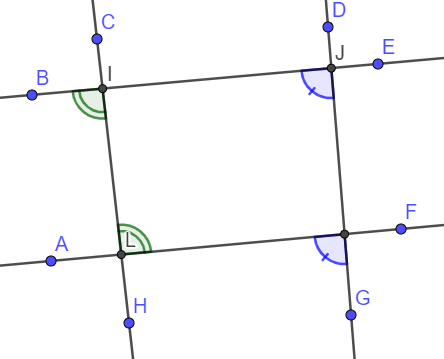
Les angles \( \widehat{ALI}\) et \( \widehat{LIJ}\) sont égaux et alterne-internes donc (BE)//(AF)

Les angles \( \widehat{BJK}\) et \( \widehat{LKG}\) sont égaux et correspondants donc (BE)//(AF)
Propriété :
Si deux angles alternes-internes (ou correspondants) sont déterminés par des droites parallèles, alors ils sont de même mesure.
Exemple :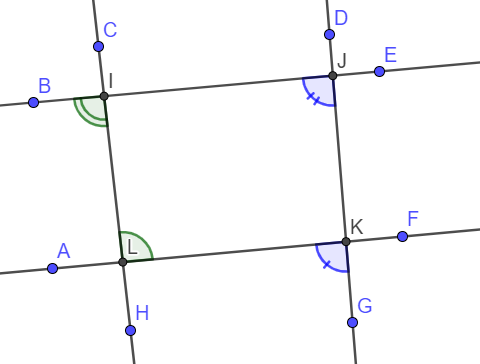
Ici, on sait que (BE)//(AF).
Or les angles BIL^ et ILK^ sont alterne-internes. Donc BIL^=ILK^

Les angles IJK^ et LKG^ sont correspondant. Donc IJK^=LKG^